組合せ 場合の数において、最重要の「組合せ」 練習問題を通じて、理解を深めましょう。 例題1 \(6\) 人を、\(a,b\) の \(2\) つの部屋に分ける。次の問いに答えなさい。 (1)\(a\) に \(4\)ならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。順列・組合せ (章末問題) → 携帯版は別頁 順列,組合せ(章末問題) → 印刷用PDF版は別頁 解説 順列 異なる n 個のものから,異なる r 個のものを取ってできる順列の総数( ただし, 0 ≦ r ≦ n ) n P r = n!(n−r)!nnnnnn
数学i Aチェック リピート 第7章 2順列 組合せ 5 三角形の個数 Pukiwiki
順列 組み合わせ 中学 問題
順列 組み合わせ 中学 問題-小学6年生の算数 場合の数・順列 練習問題プリント ツイート 組み合わせ方、並べ方を、落ちや重なりがないように順序よく整理して、調べる方法を練習できる問題プリントです。 場合の数・順列(1) 答え 場合の数・順列(2) 答え 場合の数 今回の問題は「 順列と組合せ 」です。 問題 の5つの文字がそれぞれ1つずつあるとき、次の問いに答えよ。 3つの文字を選び一列に並べるときの場合の数 3つの文字を選ぶときの場合の数 次のページ「解法のPointと問題解説」 次へ 1 2 組合せの記号 図形




順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典
よく「順列」と「組合せ」を間違って用いられている場合がありますので,慎重に扱って下さい(心の中で,順列 を扱っているのだ,組合 を扱っているのだ,という自覚をもちましょう)。 では,組み合わせの問題を考えていくことにします。整数解の個数 重複組合せの応用として整数解の個数を求める問題は超頻出です。 玉の場合と全く同じ考え方でOKです。 例題3 x y z w = 6 xyzw=6 x y z w = 6 という方程式について, (1)非負整数解の個数を求めよ。 (2)正の整数解の個数を求めよ。Spi 順列と組み合わせの問題の解き方説明 SPIの順列・組み合わせの問題は、他のSPIの問題と異なり、もう高校レベルの知識が必要になります。 このページを見る人の半数以上は、大学受験に数学を使ったきりでそれから3年以上数学に触れていない可能性も
いくつかのものからいくつかのものを取り出して 並べる ことを 順列 と呼んでいました.ここでは,取り出したときの順序を考えない場合の数を考えてみましょう.そのような問題は 組合せ の問題と呼ばれています. 順列 → → 順序を考慮 (区別)する.初めに、その問題が順列なのか、組合せなのかを見分けます。 そのために、まず「順列」と「組合せ」とは何なのか考えてみましょう。 わかりmathでは、順列の問題を「 席の問題 」、 組合せの問題を「 組の問題 」と整理しています。 順列と組合せの使い分け 問題 (1)は3つの文字を選んで、しかも一列に並べています。 これは選んだ 3つの文字に順位を付けているイメージ です。 これで1通りとなります。 ここで大事なのは このように 順位が変わったらたとえ選んだ種類が同じであっ
練習問題 10 人の生徒がいます。 以下の問に答えよ。 (1) 3 人を選ぶとき何通りの選び方がありますか。 (2) 8 人を選ぶとき何通りの選び方がありますか。 練習問題 解答へ 数学aの目次へ 数学の一般に,問題を場合分けして考えるとき,「かつ」で結ばれる個々の場合に積の法則を適用し,「または」で結ばれる全体のまとめに和の法則を適用するとよい. 相異なる3個の文字 a , b , c から2つ取るときの,組合せと順列「順列 n P r 」か「組合せ n C r 」かを判断して問題を解こう。ポイントは以下の通り。慣れれば迷わず選べるようになるよ。 POINT 区別する⇒順列 区別しない⇒組合せ 「委員2人を選ぶ」ときの場合の



同じものを含む順列の問題 京極一樹の数学塾




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
== 順列・組合せ(章末問題) == 元のHTML教材 URLhttp//wwwgeisyaorjp/~mwm461/kou3/p_c_allhtm PDF版 問題http//math2ifdefjp/p_cF 48通り 「QとRの2人を続けて並べる」という条件があるので、 まずQとRの2人を1つのグループにまとめ、 「1つのグループ」と「他の3人」の計4つの並び順 が何通りあるかを考える。 式) 4 P 4 = 4×3×2×1 = 24(通り) QとRの並び順については、「Q→R」と「R世界大百科事典 第2版 組合せ理論の用語解説 物の,組合せ的性質をもつ規則による選び方や,配列のしかたの数を考察する数学の一分野。組合せ数学とも呼ばれる。ある集合からいくつかのものを選び出す方法が何通りあるかを調べる順列・組合せの問題,多くの変数がいくつかの一次不等




同じものを含む順列と組合せは 同じ です 問題4選もあわせて解説 遊ぶ数学



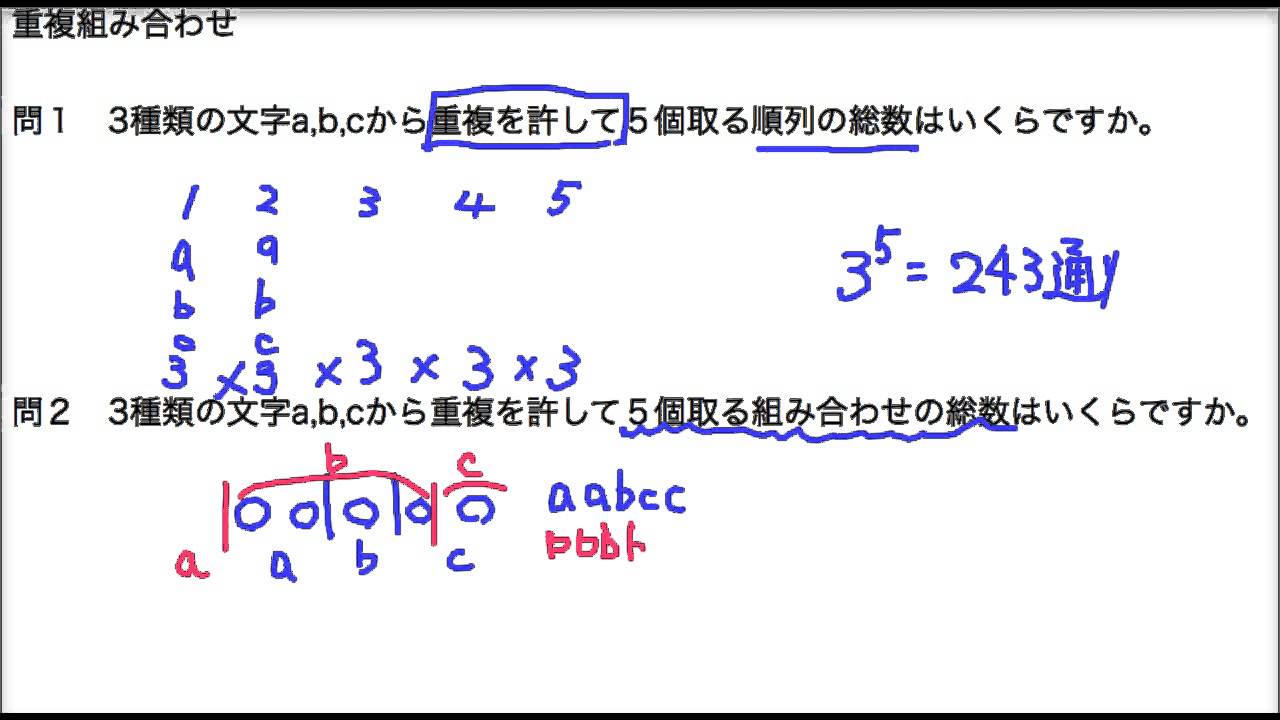
重複組合せ
ということは、これを式で表すと、 (組合せ)×2! = (順列) この問題の場合、順列は 10 P 2 だったから、 (組合せ)×2! = 10 P 2 ⇔ (組合せ)= 10 P 2 /2! 組合せ が 順列を階乗で割ったもの になったね! n C r の公式の意味がわかったかな?順列と組合せ 11 順列 111 場合の数の求め方 有限の離散標本空間に関る確率の問題などでは,標本の集合や,部分集合を数える作業 が生じる. 場合の数を,もれなく,重複もなく,順序正しく数える方法を知る必要がある. 和の法則順列・組合せ総合問題 練習問題19 5人の旅客が3件の旅館に泊まる泊まり方は何通りあるか。 ただし1人も宿泊しない旅館があってもよいとする。 上の問題において,人を仮に固定し,どの旅館に宿泊するか,ということを考えればよいのです。 発想の




高校数学a 同じものを含む順列 映像授業のtry It トライイット



数a順列組み合わせ 2番と3番の問題について なぜ分数になる Yahoo 知恵袋
SPI 場合の数 問題31(順列)Study Pro(SPI) TOP SPI言語 SPI非言語 SPI英語 CAB 構造的把握力 TOP SPI非言語 場合の数問題にしないで取り出し方だけを問題にして考えます。 したがって、順序が問題になる取り出し方の場合は順列で、順序が問題に ならない取り出し方の場合は組合せで考えればいいわけです。 では、問題を考えてみましょう。




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




順列と組み合わせの公式とその違い 問題付き 理系ラボ



数学i Aチェック リピート 第7章 2順列 組合せ 2 円順列 Pukiwiki



数学i Aチェック リピート 第7章 2順列 組合せ 10 最短経路 Pukiwiki




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




北海道札幌厚別高等学校 数学応用 学校設定科目 順列 組合せの違いを理解する 竹之内 康秀教諭




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ



数学i Aチェック リピート 第7章 2順列 組合せ 5 三角形の個数 Pukiwiki




高校数学a 同じものを含む順列 N P Q R 受験の月




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



Spi M54e217p7lcis9d Com Jyunretu Kumiawase Q1



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




順列と組み合わせの公式とその違い 問題付き 理系ラボ




Spi 非言語問題 順列 組み合わせの応用 就活の答え




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん



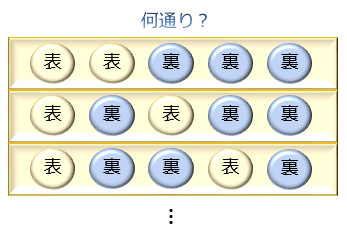
重複組み合わせは絵を描けば理解できる イラストで解説 理数白書



数学i Aチェック リピート 第7章 2順列 組合せ 1 重複順列 順列 Pukiwiki




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ



重複順列 Itパスポート出題テーマ別過去問題 平成24年度秋期 テクノロジ系 問78




二項定理 二項定理のための 順列 組合せ 大人が学び直す数学




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学



数学i Aチェック リピート 第7章 2順列 組合せ 8 同じものを含む順列 Pukiwiki



1




順列と組み合わせ 問題と解決策を含む完全な概要 Lambdageeks




高校数学a Npr と Ncr の使い分け 練習編 映像授業のtry It トライイット




高1 数a 場合の数 4 組合せ 高校生 数学のノート Clear




場合の数27 第2種スターリング数5 漸化式の証明 怜悧玲瓏 高校数学を天空から俯瞰する



数学i Aチェック リピート 第7章 2順列 組合せ 3 Ncr Pukiwiki




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




15年10月 怜悧玲瓏 高校数学を天空から俯瞰する




数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube



2




組み合わせの考え応用 最短経路選択問題をシミュレーターで理解しよう 数学入門




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




順列と組み合わせ 算数用語集




場合の数 順列 組合せ のブログ記事一覧 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




Spi 数学 対策問題 組み合わせ 順列 しかくのいろは



確率問題全般 京極一樹の数学塾



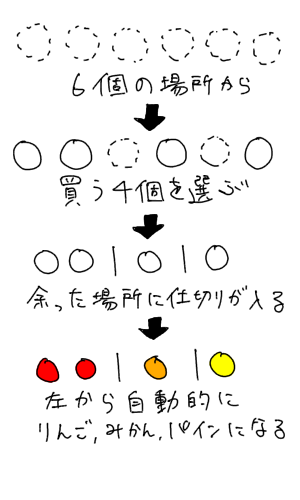
重複組み合わせ1 順列と組み合わせの違い Youtube




原田 浩明 Sサクシード223 組に分ける問題 同じものを含む順列 高校 数学 数a 組合せ



1



同じものを含む順列の問題 京極一樹の数学塾



組み合わせ C とは 公式や計算方法 は何通り 受験辞典



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




応用問題 場合の数6 同じものを含む順列と重複組み合わせ 重複組み合わせ 整数解 No Youtube




数学a確率 2 順列 組合せと確率 高校数学 解説授業 Powerpoint映像授業 Youtube




高校数学a 重複組合せ Nhr 受験の月




重複組合せ 組合せ 重複順列に関する問題 2018年度前期日程高知工科大学の入試問題 身勝手な主張




順列と組み合わせの公式とその違い 問題付き 理系ラボ



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




順列と組み合わせの公式とその違い 問題付き 理系ラボ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ
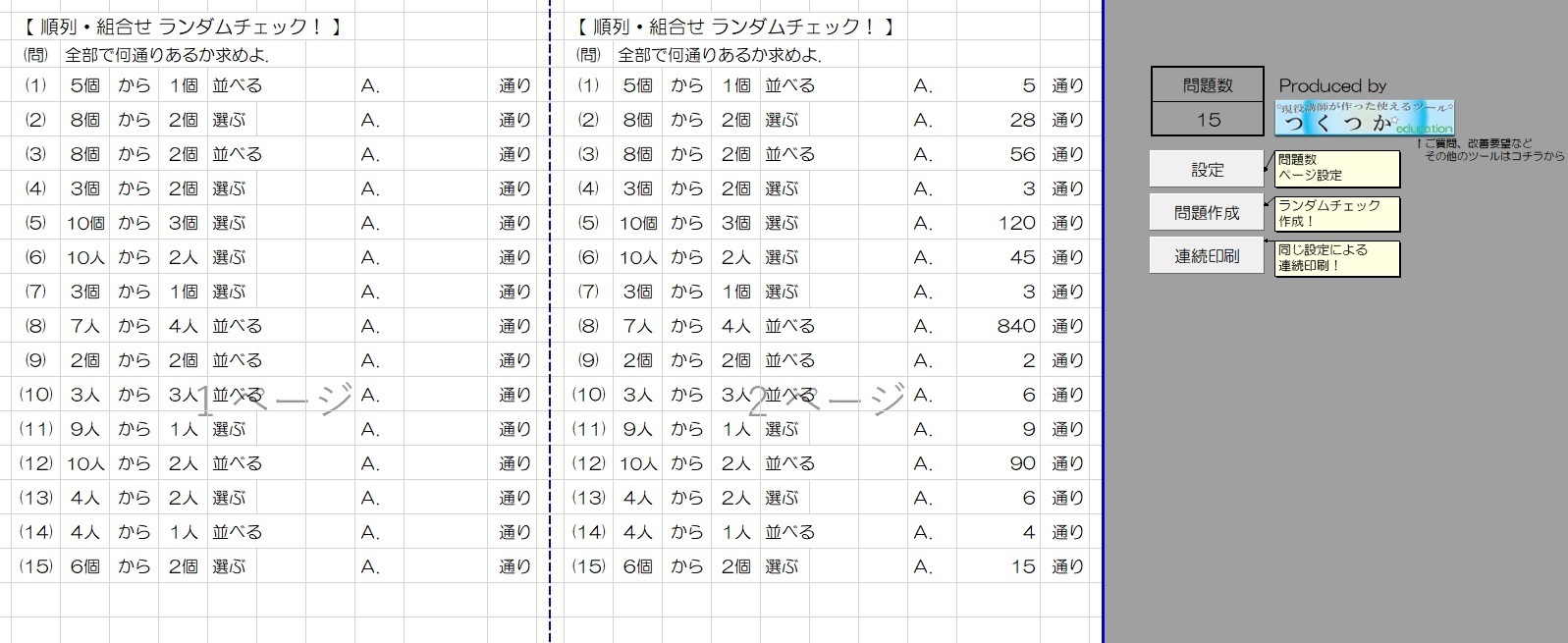



順列 組合せランダムチェック公開 現役講師が作った使えるサイト




順列と組み合わせの公式とその違い 問題付き 理系ラボ



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




重複組み合わせの問題を解くたった1つの方法とは 公式hは使用注意




高校数学a 組合せの基本と順列との関係 Ncrの性質 受験の月




順列 組み合わせ 問題は 子供達は大好きです イメージ図で簡単に解けるんです 七田式天六教室 本町教室及び魔法の折り紙オンライン教室は算数 数学のスペシャリストを育てます




高校数学 数a 7 順列 基本編 Youtube



1




高校数学a 一定の順序を含む順列 受験の月



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




場合の数 順列 組合せ のブログ記事一覧 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




順列 組み合わせ 階乗とは わかりやすくまとめてみた 数学 もんプロ 問題発見と解決のためのプログラミング



場合の数 学び家 Com




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




高校数学a 組合せの計算1 Ncr 例題編 映像授業のtry It トライイット




3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




中学数学 場合の数




順列pと組み合わせcの違いと 簡単 な見分け方




円順列の応用問題5選 難問2選を解説 順列との違いとは 遊ぶ数学




順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典




重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学




組分け問題全パターン おいしい数学




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun
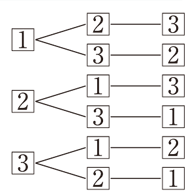



順列と組み合わせ 算数用語集




2度解く 確率 順列と組合せ 大学入試過去問シリーズp O D 版 旺文社 本 通販 Amazon



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b
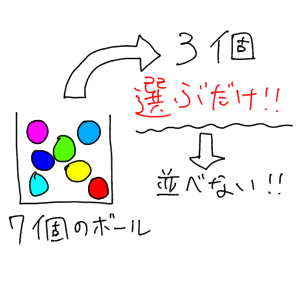



組み合わせ 並べない順列のこと 考え方と計算方法を解説 理数白書



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




順列と組み合わせの公式とその違い 問題付き 理系ラボ



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b



順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生



数学i Aチェック リピート 第7章 2順列 組合せ 6 重複組合せ Pukiwiki



1




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




順列と組合せの違いと例題 高校数学の美しい物語




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




場合の数 重複組合せ と 重複順列 の違いをわかりやすく解説します



順列と組み合わせの違いを基礎からわかりやすく解説 Youtube




重複順列の問題6選とは 公式よりも応用問題の解き方が大切です 遊ぶ数学




北海道札幌厚別高等学校 数学応用 学校設定科目 順列 組合せの違いを理解する 竹之内 康秀教諭



順列と組み合わせの違い カンタンな見分け方を教えます Studyplus スタディプラス



0 件のコメント:
コメントを投稿